
21 Đề thi vào lớp 10 môn Toán
1
TUYỂN TẬP ĐỀ THI VÀO LỚP 10
MÔN TOÁN
ĐỀ SỐ 01
Bài 1.(2điểm)
a) Thực hiện phép tính:
1 2 1 2 : 72
1 2 1 2
− +
−
+ −
b) Tìm các giá trị của m để hàm số
( )
2 3y m x= − +
đồng biến.
Bài 2. (2điểm)
a) Giải phương trình :
4 2
24 25 0x x− − =
b) Giải hệ phương trình:
2 2
9 8 34
x y
x y
− =
+ =
Bài 3. (2điểm)
Cho phương trình ẩn x :
2
5 2 0x x m− + − =
(1)
a) Giải phương trình (1) khi m =
4−
.
b) Tìm m để phương trình (1) có hai nghiệm dương phân biệt x
1
; x
2
thoả
mãn hệ thức
1 2
1 1
2 3
x x
+ =
Bài 4. (4điểm)
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của
. tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) ( với F là tiếp điểm),
tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Biết AF =
4
3
R
.
a) Chứng minh tứ giác OBDF nội tiếp. Định tâm I đường tròn ngoại tiếp tứ
giác OBDF.
b) Tính Cos
DAB
.
c) Kẻ OM ⊥ BC ( M ∈ AD) . Chứng minh
1
BD DM
DM AM
− =
d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O)
theo R.
HẾT
2
BÀI GIẢI CHI TIẾT VÀ ĐÁP ÁN ĐỀ SỐ 01
A. BÀI GIẢI CHI TIẾT VÀ ĐÁP ÁN ĐỀ SỐ 01:
BÀI GIẢI CHI TIẾT ĐIỂM
Bài 1: (2điểm)
a) Thực hiện phép tính:
1 2 1 2 : 72
1 2 1 2
− +
−
+ −
=
( ) ( )
( )( )
2 2
1 2 1 2 : 36.2
1 2 1 2
− − +
+ −
=
1 2 2 2 (1 2 2 2) :6 2
1 2
− + − + +
−
=
1 2 2 2 1 2 2 2) :6 2
1
− + − − −
−
=
4 2 2
3
6 2 =
b) Hàm số
( )
2 3y m x= − +
đồng biến
⇔
0
2 0
m
m
≥
− >
⇔
0
2
m
m
≥
>
0
4
m
m
≥
⇔
>
4m⇔ >
Bài 2: (2 điểm)
a) Giải phương trình :
4 2
24 25 0x x− − =
Đặt t = x
2
( t
0≥
), ta được phương trình :
2
24 25 0t t− − =
2
' '
b ac
∆ = −
= 12
2
–(–25)
= 144 + 25
= 169
'
13⇒∆ =
0,25 đ
0,25đ
0,25đ
0,25đ
0,5đ
{
0,25
đ
0,25đ
0,25đ
0,25đ
3
' '
1
12 13 25
1
b
ta
− + ∆ +
= = =
(TMĐK),
' '
2
12 13 1
1
b
ta
− − ∆ −
= = = −
(loại)
Do đó: x
2
= 25
5x⇒= ±
.
Tập nghiệm của phương trình :
{
}
5;5S= −
b) Giải hệ phương trình:
2 2
9 8 34
x y
x y
− =
+ =
⇔
16 8 16
9 8 34
x y
x y
− =
+ =
⇔
25 50
2 2
x
x y
=
− =
⇔
2
2.2 2
x
y
=
− =
⇔
2
2
x
y
=
=
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
Bài 3: PT:
2
5 2 0x x m− + − = (1)
a) Khi m = – 4 ta có phương trình: x
2
– 5x – 6 = 0.
Phương trình có a – b + c = 1 – (– 5) + (– 6) = 0
1 2
6
1, 6
1
c
x x a
−
⇒= − = − = − =
.
b) PT:
2
5 2 0x x m− + − =
(1) có hai nghiệm dương phân biệt
1 2
1 2
0
0
. 0
x x
x x
∆ >
⇔ + >
>
⇔
( ) ( )
( )
2
5 4 2 0
50
12 0
m
m
− − − >
− −
>
− >
33 4 0
2
m
m
− >
⇔>
33 33
2
44
2
mm
m
<
⇔ ⇔ < <
>
(*)
•
1 2
1 1
2 3
x x
+ =
2 1 1 2
3
2
x x x x
⇔ + =
( )
2
2
2 1 1 2
3
2
x x x x
⇔ + =
1 2 1 2 1 2
9
24
x x x x x x
⇔ + + =
( )
9
5 2 2 2
4
m m⇔ + − = −
0,25đ
0,5đ
0,25đ
0,25đ
0,25đ
0,25đ
4
N
I
x
D
M
O
F
C
BA
Đặt
( )
2 0t m t= − ≥
ta được phương trình ẩn t : 9t
2
– 8t – 20 = 0 .
Giải phương trình này ta được: t
1
= 2 > 0 (nhận), t
2
=
10 0
9
− <
(loại)
Vậy:
2 2m− = ⇒
m = 6 ( thỏa mãn *)
Bài 4. (4điểm)
- Vẽ hình 0,5 điểm)
a) Chứng minh tứ giác OBDF nội tiếp.
Định tâm I đường tròn ngoại tiếp tứ OBDF.
Ta có:
0
90DBO =
và
0
90DFO =
(tính chất tiếp tuyến)
Tứ giác OBDF có
0
180DBO DFO+ =
nên nội tiếp được trong một
đường tròn.
Tâm I đường tròn ngoại tiếp tứ giác OBDF là trung điểm của
OD
b) Tính Cos
DAB
.
Áp dụng định lí Pi-ta-go cho tam giác OFA vuông ở F ta
được:
2
2 2 2
4 5
OF AF 3 3
R R
OA R
= + = + =
Cos FAO =
AF 4 5
: 0,8
OA 3 3
R R
= =
osDAB 0,8C⇒=
c) Kẻ OM ⊥ BC ( M ∈ AD) . Chứng minh
1
BD DM
DM AM
− =
∗
OM // BD ( cùng vuông góc BC)
MOD BDO
⇒=
(so le trong)
và
BDO ODM
=
(tính chất hai tiếp tuyến cắt nhau)
Suy ra:
MDO MOD
=
.
Vậy tam giác MDO cân ở M. Do đó: MD = MO
∗ Áp dụng hệ quả định lí Ta let vào tam giác ABD có OM //
BD ta được:
BD AD
OM AM
=
hay
BD AD
DM AM
=
(vì MD = MO)
BD AM DM
DM AM
+
⇒
=
= 1 +
DM
AM
Do đó:
1
BD DM
DM AM
− =
(đpcm)
d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường
tròn (O) theo R.
0,25đ
0,25đ
{
0,25
đ
0,25đ
0,25đ
0,25đ
0,25đ
0,25đ
{
0,25
đ
0,25đ
0,25đ
0,25đ
5
∗
Áp dụng hệ thức lượng cho tam giác OAM vuông ở O có OF
⊥
AM ta được:
OF
2
= MF. AF hay R
2
= MF.
4
3
R⇒
MF =
3
4
R
∗
Áp dụng định lí pi ta go cho tam giác MFO vuông tại F ta được:
OM =
2
2 2 2
3 5
OF 4 4
R R
MF R
+ = + =
∗
OM // BD
OM AO
BD AB
⇒=.OM AB
BD OA
⇒=
=
5 5 5
. : 2
4 3 3
R R R
R R
+ =
Gọi S là diện tích phần hình tứ giác OBDM ở bên ngoài nửa
đường tròn (O) .
S
1
là diện tích hình thang OBDM.
S
2
là diện tích hình quạt góc ở tâm
0
90BON =
Ta có: S = S
1
– S
2
.
( )
1
1.
2
S OM BD OB= +
=
2
1 5 13
2 .
2 4 8
R R
R R
+ =
(đvdt)
2 0 2
20
.90
360 4
R R
S
π π
= =
(đvdt)
Vậy S = S
1
– S
2
=
2 2
13
8 4
R R
π
−
=
( )
2
13 2
8
R
π
−
(đvdt)
hết
Lưu ý:Bài toán hình có nhiều cách giải .Có thể các em sẽ tìm nhiều cách giải hay
hơn
.
0,25đ
0,25đ
0,25đ
6
TUYỂN TẬP ĐỀ THI VÀO LỚP 10
MÔN TOÁN
Bài 1. ( 2điểm)
Rút gọn các biểu thức sau:
a)
3 5
15 5 3
+
b)
( )( )
11 3 1 1 3+ + −
Bài 2. ( 1,5điểm)
Giải các phương trình sau:
a) x
3
– 5x = 0 b)
1 3x− =
Bài 3. (2điểm)
Cho hệ phương trình :
2 5
3 0
x my
x y
+ =
− =
( I )
a) Giải hệ phương trình khi m = 0 .
b) Tìm giá trị của m để hệ (I) có nghiệm ( x; y) thoả mãn hệ thức:
m+1
x - y + 4
m-2 = −
Bài 4. ( 4,5điểm).
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O đường kính AM=2R.
Gọi H là trực tâm tam giác .
a) Chứng minh tứ giác BHCM là hình bình hành.
b) Gọi N là điểm đối xứng của M qua AB. Chứng minh tứ giác
AHBN
nội tiếp được trong một đường tròn.
c) Gọi E là điểm đối xứng của M qua AC. Chứng minh ba điểm N,H,E
thẳng hàng.
d) Giả sử AB = R
3
. Tính diện tích phần chung của đưòng tròn (O) và
đường tròn ngoại tiếp tứ giác AHBN.
HẾT
ĐỀ SỐ 02
có thể bạn quan tâm

Các nguyên tắc kế toán chung được kế toán thừa nhận khi hạch toán kế...
2
807
354
Kế toán, kiểm toán
2
(New)
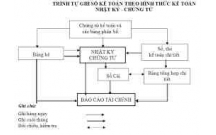
Hạch toán kế toán theo Hình thức kế toán - Nhật ký chứng từ
2
873
328
Kế toán, kiểm toán
2
(New)

Toán nâng cao bồi dưỡng học sinh giỏi toán lớp 2: Bài toán về nhiều hơ...
4
7.820
721
Tài liệu, đề thi môn Toán
4
(New)

CHUẨN MỰC KẾ TOÁN: THAY ĐỔI CHÍNH SÁCH KẾ TOÁN, ƯỚC TÍNH KẾ TOÁN VÀ C...
30
770
306
Kế toán, kiểm toán
30
(New)

Luận văn: kiểm toán thuế trong kiểm toán báo cáo tài chính tại các DN...
87
892
374
Kinh tế quản lý
87
(New)

Luận văn: Cty TNHH Trang Quang- kế toán NVL và thực trạng công tác hạc...
76
815
356
Kinh tế quản lý
76
(New)
Bài toán nâng cao bồi dưỡng học sinh năng khiếu Toán 2: Một số bài toá...
4
1.439
370
Tài liệu, đề thi môn Toán
4
(New)

Luận văn: Cty TNHH Kiểm Toán Mỹ- Khái quát quy trình kiểm toán BCTC và...
161
910
337
Thạc sĩ cao học
161
(New)
thông tin tài liệu
Đề thi tuyển sinh lớp 10 môn Toán | 21 Đề thi vào lớp 10 môn Toán bao gồm 21 đề thi môn toán vào lớp 10 được Tailieu123 sưu tầm có đáp án chi tiết, rõ ràng, là tài liệu ôn thi môn Toán vào lớp 10 hiệu quả dành cho các em THCS. Mời các em học sinh lớp 9 tải bộ đề thi vào lớp 10 này về để luyện tập, ôn thi thật tốt trước kỳ thi vào lớp 10 năm học 2018 - 2019.
Mở rộng để xem thêm
tài liệu mới trong mục này
Giải bài tập trang 144 SGK Hóa lớp 9: Mối liên hệ giữa etilen, rượu etylic và axit axetic
Giải bài tập Hóa lớp 9: Rượu etylic
Giải bài tập Hóa lớp 9: Khái niệm về hợp chất hữu cơ và hoá học hữu cơ
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm giá trị phần trăm một số
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm tỉ số phần trăm của hai số
tài liệu hot trong mục này
Ôn tập kiến thức môn Toán lớp 2 chuyên đề: Phép cộng có nhớ
Bộ đề thi giữa học kì 1 môn Toán lớp 2 theo Thông tư 22
Một số dạng bài tập về Phép cộng, trừ các số nguyên trong chương trình Toán lớp 6
Bài tập ôn tập cuối tuần lớp 2: Tuần 21
Lý thuyết và một số dạng bài tập về Lũy thừa với số mũ tự nhiên và các phép toán (Toán lớp 6)
tài liệu giúp tôi
Nếu bạn không tìm thấy tài liệu mình cần có thể gửi yêu cầu ở đây để chúng tôi tìm giúp bạn!
xem nhiều trong tuần
Hướng dẫn cài đăt lại Windows 7 OEM loai trừ bloatware cho máy tính
Triệu phú thầm lặng
Một số tính năng ẩn trong hệ điều hành Windows 8
10 đề speaking mới ra tháng 9 - tháng 12 ( tỷ lệ ra nhiều nhất)
Hướng dẫn bảo mật tài khoản Google với Google Authenticator
Cách sử dụng biểu tượng trong Microsoft Word 2013
yêu cầu tài liệu
Giúp bạn tìm tài liệu chưa có
×



