Home
Giáo dục đào tạo
Tài liệu, đề thi môn Toán
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Một số tiêu chuẩn nhận biết tứ giác nội tiếp
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Một số tiêu chuẩn nhận biết tứ giác nội tiếp
MỘT SỐ TIÊU CHUẨN NHẬN BIẾT TỨ GIÁC NỘI TIẾP
Tiêu chuẩn 1. Điều kiện cần và đủ để bốn đỉnh của một tứ
giác lồi nằm trên cùng một đường tròn là tổng số đo của hai
góc tứ giác tại hai đỉnh đối diện bằng
0
180
.
Điều kiện để tứ giác lồi
ABCD
nội tiếp là:
0
A C 180
hoặc
0
B D 180
Hệ quả: Tứ giác
ABCD
nội tiếp được
BAD DCx
Một số ví dụ
Ví dụ 1: Cho tam giác
ABC
vuông tại
A
. Kẻ đường cao
AH
và phân giác trong
AD
của góc
HAC
. Phân giác trong góc
ABC
cắt
AH,AD
lần lượt tại
M,N
. Chứng minh rằng:
0
BND 90
.
Phân tích và hướng dẫn giải:
Ta có
0
MHD 90
. Nếu
0
MND 90
thì tứ giác
MHDN
nội tiếp. Vì vậy
thay vì trực tiếp chỉ ra góc
0
BND 90
ta sẽ đi chứng minh
tứ giác
MHDN
nội tiếp. Tức là ta chứng minh
AMN ADH
.
Thật vậy ta có
0
AMN BMH 90 MBH
,
0
NDH 90 HAD
mà
1 1
MBH ABC,HAD HAC
2 2
và
ABC HAC
do cùng phụ với góc
BCA
từ đó suy ra
AMN ADH
hay tứ giác
MHDN
nội tiếp
0
MND MHD 90
x
D
C
B
A
D
H
N
M
C
B
A
Ví dụ 2: Cho tam giác
ABC
có 3 góc nhọn nội tiếp đường
tròn
(O)
có trực tâm là điểm
H
. Gọi
M
là điểm trên dây cung
BC
không chứa điểm
A
(
M
khác
B,C
). Gọi
N,P
theo thứ tự là
các điểm đối xứng của
M
qua các đường thẳng
AB,AC
a) Chứng minh
AHCP
là tứ giác nội tiếp
b)
N,H,P
thẳng hàng.
c) Tìm vị trí của điểm
M
để độ dài đoạn
NP
lớn nhất.
Phân tích và hướng dẫn giải:
a). Giả sử các đường cao của tam giác là
AK,CI
. Để chứng
minh
AHCP
là tứ giác nội tiếp ta sẽ chứng minh
0
AHC APC 180
.Mặt khác ta có
AHC IHK
( đối đỉnh),
APC AMC ABC
( do tính đối xứng và góc nội tiếp cùng chắn
một cung). Như vậy ta chỉ cần chứng minh
0
ABC IHK 180
nhưng điều này là hiển nhiên do tứ giác
BIHK
là tứ giác nội
tiếp.
b). Để chứng minh
N,H,P
thẳng hàng ta sẽ chứng minh
0
NHA AHP 180
do đó ta sẽ tìm cách quy hai góc này về 2
góc đối nhau trong một tứ giác nội tiếp.
Thật vậy ta có:
AHP ACP
(tính chất góc nội tiếp),
ACP ACM
(1) (Tính chất đối xứng) . Ta thấy vai trò tứ giác
AHCP
giống
với
AHBN
nên ta cũng dễ chứng minh được
AHBN
là tứ giác
nội tiếp từ đó suy ra
AHN ABN
, mặt khác
ABN ABM
(2)
O
N
P
H
I
K
B
M
C
A
(Tính chất đối xứng) . Từ (1), (2) ta suy ra chỉ cần chứng
minh
0
ABM ACM 180
nhưng điều này là hiển nhiên do tứ
giác
ABMC
nội tiếp. Vậy
0
NHA AHP 180
hay
N,H,P
thẳng
hàng.
Chú ý: Đường thẳng qua
N,H,P
chính là đường thẳng
Steiners của điểm
M
. Thông qua bài toán này các em học
sinh cần nhớ tính chất. Đường thẳng Steiners của tam giác
thì đi qua trực tâm của tam giác đó . (Xem thêm phần “Các
định lý hình học nổi tiếng’’).
c). Ta có
MAN 2BAM,MAP 2MAC NAP 2BAC
. Mặt khác ta
có
AM AN AP
nên các điểm
M,N,P
thuộc đường tròn tâm
A
bán kính
AM
. Áp dụng định lý sin trong tam giác
NAP
ta
có:
NP 2R.sinNAP 2AM.sin2BAC
. Như vậy
NP
lớn nhất khi và
chỉ khi
AM
lớn nhất. Hay
AM
là đường kính của đường tròn
(O)
Ví dụ 3: Cho tam giác
ABC
và đường cao
AH
gọi
M,N
lần
lượt là trung điểm của
AB,AC
. Đường tròn ngoại tiếp tam
giác
BHM
cắt đường tròn ngoại tiếp tam giác
CNH
tại
E
.
Chứng minh
AMEN
là tứ giác nội tiếp và
HE
đi qua trung
điểm của
MN
.
Phân tích, định hướng cách giải:
Để chứng minh
AMEN
là tứ giác nội tiếp ta sẽ
chứng minh:
0
MAN MEN 180
.
Ta cần tìm sự liên hệ của các góc
MAN;MEN
với các góc có sẵn
của những tứ giác nội tiếp khác.
Ta có
0 0 0 0
MEN 360 MEH NEH 360 180 ABC 180 ACB ABC ACB
0
180 BAC
suy ra
0
MEN MAN 180
. Hay tứ giác
AMEN
là tứ
giác nội tiếp.
K
E
I
H
N
M
C
B
A
Kẻ
MK BC
, giả sử
HE
cắt
MN
tại
I
thì
IH
là cát tuyến của
hai đường tròn
(BMH)
,
(CNH)
. Lại có
MB MH MA
(Tính chất
trung tuyến tam giác vuông). Suy ra tam giác
MBH
cân tại
M KB KH MK
luôn đi qua tâm đường tròn ngoại tiếp tam
giác
MBH
. Hay
MN
là tiếp tuyến của
(MBH)
suy ra
2
IM IE.IH
,
tương tự ta cũng có
MN
là tiếp tuyến của
HNC
suy ra
2
IN IE.IH
do đó
IM IN
.
Xem thêm phần: ‘’Các tính chất của cát tuyến và tiếp tuyến’’
Ví dụ 4) Cho tam giác cân
ABC
(AB AC)
P
là điểm trên cạnh
đáy
BC
. Kẻ các đường thẳng
PE,PD
lần lượt song song với
AB,AC E AC,D AB
gọi
Q
là điểm đối xứng với
P
qua
DE
.
Chứng minh bốn điểm
Q,A,B,C
cùng thuộc một đường tròn.
Phân tích định hướng giải:
Bài toán có 2 giả thiết cần lưu ý.
Đó là các đường thẳng song song
với 2 cạnh tam giác , và điểm
Q
đối xứng với
P
qua
DE
.
Do đó ta sẽ có:
AD EP EC EQ
và
DP DQ
( Đây là chìa khóa để ta giải bài toán này)
Từ định hướng đó ta có lời giải như sau: Do
AD / /PE,PD / /AE ADPE
là hình bình hành
AE DP DQ
. Mặt khác do
P,Q
đối xứng nhau qua
DE AD PE EQ
. Suy ra
DAQE
là hình thang cân
DAQ AQE
. Kéo dài
DE
cắt
CQ
tại
H
ta có
DAQ AQE PEH
.
Như vậy để chứng minh
ABCQ
nội tiếp ta cần chứng minh:
0
PCH PEH 180 PEHC
là tứ giác nội tiếp. Mặt khác ta có:
ECQ EQC
(do tam giác
EQC
cân),
EPH EQH
(Do tính đối xứng
) suy ra
ECH EPH EPCH
là tứ giác nội tiếp.
H
E
I
Q
P
D
C
B
A
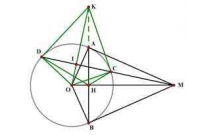
Ví dụ 5) Cho tam giác
ABC
nội tiếp đường tròn
O
. Dựng
đường tròn qua
B
và tiếp xúc với cạnh
AC
tại
A
dựng đường
tròn qua
C
và tiếp xúc với
AB
tại
A
hai đường tròn này cắt
nhau tại
D
. Chứng minh
0
ADO 90
Phân tích định hướng giải:
Ta thấy rằng
0
ADO 90
thì các điểm
A,D,O
cùng nằm trên đường tròn
đường kính
OA
.Ta mong muốn tìm
ra được một góc bằng
0
ADO 90
.
Điều này làm ta nghỉ đến tính chất
quen thuộc ‘’Đường kính đi qua trung
điểm của một dây cung thì vuông góc
với dây đó’’. Vì vậy nếu ta gọi
M,N
là trung điểm của
AB,AC
thì ta sẽ có:
0
OMA ONA 90
. Do đó tứ giác
OMAN
nội tiếp. Công việc còn
lại là ta chứng minh
AMDO
hoặc
ANOD
hoặc
DMAN
là tứ
giác nội tiếp. Mặt khác ta có:
ABD CAD
và
ACD BAD
(Tính
chất góc tạo bởi tiếp tuyến và dây cung)
BDA
và
ADC
đồng dạng nên ta suy ra
DMA DNC
0
DMA DNA DNC DNA 180
AMDN
nội tiếp suy ra năm
điểm
A,M,D,O,N
nằm trên đường tròn đường kính
OA
0
ADO 90
Ví dụ 6: Cho tam giác
ABC
vuông cân tại
A
một đường tròn
O
tiếp xúc với
AB,AC
tại
B,C
. Trên cung
BC
nằm trong tam
giác
ABC
lấy một điểm
M
M B;C
. Gọi
I,H,K
lần lượt là hình
chiếu của
M
trên
BC;CA;AB
và
P
là giao điểm của
MB
với
IK,
Q
là giao điểm của
MC
với
IH
. Chứng minh
PQ / /BC
.
Phân tích định hướng giải:
Để chứng minh
PQ / /BC
D
O
C
N
M
B
A
A
B
C
K
I
M
P
Q
O
H
ta chứng minh
MPQ MBC
nhưng tứ giác
BIMK
nội tiếp
nên
MBC MKI
. Mặt khác
AC
là tiếp tuyến của
(O)
nên
ta có:
ACK MBC
và
CIMH
nội tiếp nên
ACK MIH
.Như vậy để chứng minh
PQ / /BC
ta
cần chứng minh
MIH MPQ
. Tức là ta cần chứng minh tứ giác
MPIQ
nội tiếp . Để ý rằng
0
BMC KMH 135
,
PIQ PIM IMQ
0
1
KBM KCH sđ BM MC 45
2
suy ra đpcm.(Các em học
sinh tự hoàn thiện lời giải)
Tiêu chuẩn 2: Tứ giác
ABCD
nội tiếp
ADB ACB
Ví dụ 1. Trên các cạnh
BC,CD
của hình vuông
ABCD
ta lấy
lần lượt các điểm
M,N
sao cho
0
MAN 45
. Đường thẳng
BD
cắt các đường thẳng
AM,AN
tương ứng tại các điểm
P,Q
.
a) Chứng minh rằng các tứ giác
ABMQ
và
ADNP
nội tiếp.
b) Chứng minh rằng các điểm
M,N,Q,P,C
nằm trên cùng một
đường tròn.
Lời giải:
a). Gọi
E
là giao điểm của
AN
và
BC
.
Các điểm
M
và
Q
nằm trên hai cạnh
EB
và
EA
của tam giác
EBA
, nên tứ giác
ABMQ
là lồi. Các đỉnh
A
và
B
cùng
O
D
C
B
A
E
N
M
Q
P
D
C
B
A
có thể bạn quan tâm
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Hệ thức lượng trong tam...
55
1.006
326
Tài liệu, đề thi môn Toán
55
(New)
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Chùm bài tập về tiếp tu...
11
2.922
497
Tài liệu, đề thi môn Toán
11
(New)
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Những định lý hình học...
39
1.160
436
Tài liệu, đề thi môn Toán
39
(New)
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Chương 2 Hình Tròn
26
1.093
335
Tài liệu, đề thi môn Toán
26
(New)
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Một số bài tập chọn lọc...
43
869
313
Tài liệu, đề thi môn Toán
43
(New)
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Chương 3: Góc với đường...
22
1.133
357
Tài liệu, đề thi môn Toán
22
(New)
BÀI TẬP DÀNH CHO HỌC SINH GIỎI MÔN TOÁN - LỚP 2 CHUYÊN ĐỀ PHÉP NHÂN
1
2.813
488
Tài liệu, đề thi môn Toán
1
(New)
Tiểu luận: Nhận thức về bồi dưỡng các chuyên đề kiến thức Quốc phòng A...
2
796
348
Lý luận chính trị
2
(New)
thông tin tài liệu
Lý thuyết tổng hợp về tứ giác nội tiếp, một số tiêu chuẩn nhận biết tứ giác nội tiếp có ví dụ minh họa cụ thể.
Mở rộng để xem thêm
tài liệu mới trong mục này
Giải bài tập trang 144 SGK Hóa lớp 9: Mối liên hệ giữa etilen, rượu etylic và axit axetic
Giải bài tập Hóa lớp 9: Rượu etylic
Giải bài tập Hóa lớp 9: Khái niệm về hợp chất hữu cơ và hoá học hữu cơ
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm giá trị phần trăm một số
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm tỉ số phần trăm của hai số
tài liệu hot trong mục này
Ôn tập kiến thức môn Toán lớp 2 chuyên đề: Phép cộng có nhớ
Bộ đề thi giữa học kì 1 môn Toán lớp 2 theo Thông tư 22
Một số dạng bài tập về Phép cộng, trừ các số nguyên trong chương trình Toán lớp 6
Bài tập ôn tập cuối tuần lớp 2: Tuần 21
Lý thuyết và một số dạng bài tập về Lũy thừa với số mũ tự nhiên và các phép toán (Toán lớp 6)
tài liệu giúp tôi
Nếu bạn không tìm thấy tài liệu mình cần có thể gửi yêu cầu ở đây để chúng tôi tìm giúp bạn!
xem nhiều trong tuần
Giáo trình Quản trị học của Đại học kinh tế quốc dân
4 đề thi học sinh giỏi Toán lớp 2, có đáp án kèm theo
Luận văn về các tác nhân ảnh hưởng đến kết quả học tập của sinh viên chính quy trường Đại Học Kinh Tế- TP HCM
Mẫu slide thuyết trình về Golf
Bài tập ôn tập cuối tuần lớp 2: Tuần 21
Bài tập ôn tập cuối tuần lớp 3: Tuần 21
yêu cầu tài liệu
Giúp bạn tìm tài liệu chưa có
×
