Home
Giáo dục đào tạo
Tài liệu, đề thi môn Toán
Đề thi tuyển sinh lớp 10 THPT năm học 2013 môn Toán - Bắc Giang
Đề thi tuyển sinh lớp 10 THPT năm học 2013 môn Toán - Bắc Giang
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI TUYỂN SINH LỚP 10 THPT
BẮC GIANG NĂM HỌC 2012-2013
Môn thi : Toán
Thời gian : 120 phút không kể thời gian giao đề
Ngày thi 30 tháng 6 năm 2012
Câu 1. (2 đ iểm)
1.Tính
12
2 1-
-
2. Xác định giá trị của a,biết đồ thị hàm số y = ax - 1 đi qua điểm M(1;5)
Câu 2: (3 đ iểm)
1.Rút gọn biểu thức:
1 2 3 2
( ).( 1)
2 2 2
a a
Aa a a a
- +
= - +
- - -
với a>0,a
4¹
2.Giải hệ pt:
53
952
yx
yx
3. Chứng minh rằng pt:
21 0x mx m+ + - =
luôn có nghiệm với mọi giá trị của m.
Giả sử x1,x2 là 2 nghiệm của pt đã cho,tìm giá trị nhỏ nhất của biểu thức
2 2
1 2 1 2
4.( )B x x x x= + - +
Câu 3: (1,5 đ iểm)
Một ôtô tải đi từ A đến B với vận tốc 40km/h. Sau 2 giờ 30 phút thì một ôtô taxi
cũng xuất phát đi từ A đến B với vận tốc 60 km/h và đến B cùng lúc với xe ôtô tải.Tính
độ dài quãng đường AB.
Câu 4: (3 đ iểm)
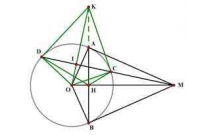
Cho đường tròn (O) và một điểm A sao cho OA=3R. Qua A kẻ 2 tiếp tuyến AP và
AQ của đường tròn (O),với P và Q là 2 tiếp điểm.Lấy M thuộc đường tròn (O) sao cho
PM song song với AQ.Gọi N là giao điểm thứ 2 của đường thẳng AM và đường tròn
(O).Tia PN cắt đường thẳng AQ tại K.
1.Chứng minh APOQ là tứ giác nội tiếp.
2.Chứng minh KA2=KN.KP
3.Kẻ đường kính QS của đường tròn (O).Chứng minh tia NS là tia phân giác của góc
PNM
.
4. Gọi G là giao điểm của 2 đường thẳng AO và PK .Tính độ dài đoạn thẳng AG theo
bán kính R.
Câu 5: (0,5 đ iểm)
Cho a,b,c là 3 số thực khác không và thoả mãn:
2 2 2
2013 2013 2013
( ) ( ) ( ) 2 0
1
a b c b c a c a b abc
abc
ì
ï+ + + + + + =
ï
í
ï+ + =
ï
î
Hãy tính giá trị của biểu thức
2013 2013 2013
1 1 1
Qabc
= + +
ĐỀ THI CHÍNH THỨC
HƯỚNG DẪN CHẤM (tham khảo)
Câu Ý Nội dung Điểm
1 1
2
1 2 1 2 1
2 2 2 2 1 2 1
2 1 ( 2 1).( 2 1) ( 2) 1)
+ +
- = - = - = + - =
- - + -
KL:
1
2 Do đồ thị hàm số y = ax-1 đi qua M(1;5) nên ta có a.1-1=5
Û
a=6
KL:
1
2 1
2 ( 1).( 2)
( ).( 1)
( 2) ( 2) 2
2 1
( ).( 1 1) . 1
( 2)
a a a
Aa a a a a
aa a
a a a
- -
= - + =
- - -
-
= - + = =
-
KL:
0,5
0,5
2
2 5 9 2 5 9 2 5 9 1
3 5 15 5 25 17 34 2
x y x y x y y
x y x y x x
ì ì ì ì
- = - = - = =-
ï ï ï ï
ï ï ï ï
Û Û Û
í í í í
ï ï ï ï
+ = + = = =
ï ï ï ï
î î î î
KL:
1
3 Xét Pt:
2
1 0x mx m+ + - =
2 2 2
Δ 4( 1) 4 4 ( 2) 0m m m m m= - - = - + = - ³
Vậy pt luôn có nghiệm với mọi m
Theo hệ thức Viet ta có
1 2
1 2
1
x x m
x x m
ì+ =-
ï
ï
í
ï= -
ï
î
Theo đề bài
2 2 2
1 2 1 2 1 2 1 2 1 2
2 2 2
2
4.( ) ( ) 2 4.( )
2( 1) 4( ) 2 2 4 2 1 1
( 1) 1 1
B x x x x x x x x x x
m m m m m m m m
m
= + - + = + - - +
= - - - - = - + + = + + +
= + + ³
Vậy minB=1 khi và chỉ khi m = -1
KL:
0,25
0,25
0,5
3 Gọi độ dài quãmg đường AB là x (km) x>0
Thời gian xe tải đi từ A đến B là
40
x
h
Thời gian xe Taxi đi từ A đến B là :
60
x
h
Do xe tải xuất phát trước 2h30phút =
5
2
nên ta có pt
0,25
0,25
0,25
0,25
5
40 60 2
3 2 300
300
x x
x x
x
- =
Û - =
Û =
Giá trị x = 300 có thoả mãn ĐK
Vậy độ dài quãng đường AB là 300 km.
0,25
0,25
4 1
G
K
N
S
M
I
Q
P
A
O
Xét tứ giác APOQ có
0
90APO =
(Do AP là tiếp tuyến của (O) ở P)
0
90AQO =
(Do AQ là tiếp tuyến của (O) ở Q)
0
180APO AQOÞ + =
,mà hai góc này là 2 góc đối nên tứ giác APOQ là tứ
giác nội tiếp
0,75
2Xét
Δ
AKN và
Δ
PAK có
AKP
là góc chung
APN AMP=
( Góc nt……cùng chắn cung NP)
Mà
NAK AMP=
(so le trong của PM //AQ
Δ
AKN ~
Δ
PKA (gg)
2
.
AK NK AK NK KP
PK AK
Þ = Þ =
(đpcm)
0,75
3 Kẻ đường kính QS của đường tròn (O)
Ta có AQ
^
QS (AQ là tt của (O) ở Q)
Mà PM//AQ (gt) nên PM
^
QS
Đường kính QS
^
PM nên QS đi qua điểm chính giữa của cung PM nhỏ
sd PS sd SM=
PNS SNMÞ =
(hai góc nt chắn 2 cung bằng nhau)
Hay NS là tia phân giác của góc PNM
0,75
4Chứng minh được
Δ
AQO vuông ở Q, có QG
^
AO(theo Tính chất 2 tiếp
tuyến cắt nhau)
Theo hệ thức lượng trong tam giác vuông ta có 0,75
2 2
21
.3 3
1 8
33 3
OQ R
OQ OI OA OI R
OA R
AI OA OI R R R
= Þ = = =
Þ = - = - =
Do
Δ
KNQ ~
Δ
KQP (gg)
2
.KQ KN KPÞ =
mà
2
.AK NK KP=
nên AK=KQ
Vậy
Δ
APQ có các trung tuyến AI và PK cắt nhau ở G nên G là trọng tâm
2 2 8 16
.
3 3 3 9
AG AI R RÞ = = =
5 Ta có:
222
2 2 2 2 2 2
2 2 2 2 2 2
2 2
2
( ) ( ) ( ) 2 0
2 0
( ) ( ) (2 ) 0
( ) ( ) ( ) 0
( )( ) 0
( ).( ).( ) 0
a b c b c a c a b abc
a b a c b c b a c a c b abc
a b b a c a c b abc b c a c
ab a b c a b c a b
a b ab c ac bc
a b a c b c
+ + + + + + =
Û + + + + + + =
Û + + + + + + =
Û + + + + + =
Û + + + + =
Û + + + =
*TH1: nếu a+ b=0
Ta có
2013 2013 2013
1
1
a b a b
c
a b c
ìì
=- =-
ïï
ï ï
Û
í í
ï ï =
+ + = ï
î
ï
î
ta có
2013 2013 2013
1 1 1 1Qabc
= + + =
Các trường hợp còn lại xét tương tự
Vậy
2013 2013 2013
1 1 1 1Qabc
= + + =
0,25
0,25
có thể bạn quan tâm
Đề thi môn toán Kì thi tuyển sinh vào lớp 10 trường THPT Hoàng văn Thụ...
12
673
315
Tài liệu, đề thi môn Toán
12
(New)
Tuyển tập toán ôn luyện dành cho học sinh giỏi Toán lớp 2
4
1.627
390
Tài liệu, đề thi môn Toán
4
(New)
Tuyển tập 50 bài toán hay bồi dưỡng học sinh giỏi lớp 4
8
2.401
543
Tài liệu, đề thi học sinh giỏi
8
(New)
Chuyên đề bồi dưỡng học sinh giỏi Hình học 9 - Chùm bài tập về tiếp tu...
11
2.892
489
Tài liệu, đề thi môn Toán
11
(New)
Đề thi thử THPT môn Sinh học TRƯỜNG THPT HƯNG ĐẠO Hải Dương
6
869
380
Tài liệu, đề thi THPT các trường
6
(New)
Đề thi thử tuyển sinh vào lớp 10 năm 2017 môn Toán Phòng GD và ĐT Tam...
4
734
320
Tài liệu, đề thi môn Toán
4
(New)
Toán lớp 1 và các dạng bài thi tuyển chọn học sinh giỏi - phần 2
8
801
363
Tài liệu, đề thi học sinh giỏi
8
(New)
SINH HỌC : Cấu tạo, chức năng của tuyến yên và tuyến giáp
3
1.158
349
Giáo án, bài giảng lớp 8
3
(New)
thông tin tài liệu
Đề thi chính thức được sử dụng trong kì thi tuyến sinh vào lớp 10 THPT năm 2013 của tỉnh Bắc Giang.
Thời gian làm bài: 120 phút
Có hướng dẫn tham khảo cách giải chi tiết
Mở rộng để xem thêm
tài liệu mới trong mục này
Giải bài tập trang 144 SGK Hóa lớp 9: Mối liên hệ giữa etilen, rượu etylic và axit axetic
Giải bài tập Hóa lớp 9: Rượu etylic
Giải bài tập Hóa lớp 9: Khái niệm về hợp chất hữu cơ và hoá học hữu cơ
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm giá trị phần trăm một số
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm tỉ số phần trăm của hai số
tài liệu hot trong mục này
Ôn tập kiến thức môn Toán lớp 2 chuyên đề: Phép cộng có nhớ
Bộ đề thi giữa học kì 1 môn Toán lớp 2 theo Thông tư 22
Một số dạng bài tập về Phép cộng, trừ các số nguyên trong chương trình Toán lớp 6
Bài tập ôn tập cuối tuần lớp 2: Tuần 21
Lý thuyết và một số dạng bài tập về Lũy thừa với số mũ tự nhiên và các phép toán (Toán lớp 6)
tài liệu giúp tôi
Nếu bạn không tìm thấy tài liệu mình cần có thể gửi yêu cầu ở đây để chúng tôi tìm giúp bạn!
×
