TOÁN LỚP 6 BỘI CHUNG NHỎ NHẤT TIẾT 1
Tiết 30: BỘI CHUNG NHỎ NHẤT
I. MỤC TIÊU BÀI HỌC:
1.Kiến thức: Học sinh hiểu được thế nào là BCNN của nhiều số.
2.Kỹ năng:
– Học sinh biết tìm BCNN của hai hay nhiều số bằng cách phân tích các
số đó ra thừa số nguyên tố, từ đó biết tìm BC của hai hay nhiều số.
– Học sinh biết phân biệt được điểm giống và khác nhau giữa hai qui tắc
tìm BCNN và ƯCLN, biết tìm BCNN một cách hợp lí trong từng trường
hợp cụ thể.
3.Thái độ: Vận dụng trong việc giải các bài toán.
II. CHUẨN BỊ TÀI LIỆU-TBDH:
1. Chuẩn bị của thầy: SGK, SGV, tài liệu tham khảo.
2. Chuẩn bị của trò: ĐDHT, SGK, phiếu học tập.
III. TIẾN TRÌNH HOẠT ĐỘNG DẠY HỌC:
1.Ổn định tổ chức:
2. Kiểm tra bài cũ:
Nêu cách tìm ƯCLN? Áp dụng tìm ƯC(18;36;72)
Đáp: ƯCLN(18;36;72) = 18 => ƯC(18;36;72) = {1;2;3;6;9;18}
3.Bài mới:
*ĐVĐ: Cách m ƯCLN chúng ta đã biết .Vậy để m BCNN ta thực hiện như thế
nào?
Hoạt động của thầy - trò Nội dung kiến thức cần đạt
Hoạt động 1: Tìm hiểu về bội chung nhỏ
nhất
GV: Cho HS thực hiện ví dụ như SGK
GV: Giới thiệu về BCNN của hai hay
nhiều số.
GV: Vậy bội chung nhỏ nhất của hai hay
nhiều số là số như thế nào?
GV: Nêu kí hiệu.
GV: Gọi HS đọc phần đóng khung
sgk/57
GV: Em có nhận xét gì về các bội chung
của 6 và 9 với BCNN(6;9)?
GV: Cho HS đọc nhận xét SGK
GV: Mọi số tự nhiên đều là gì của 1?
GV: Nêu chú ý về trường hợp tìm
1. Bội chung nhỏ nhất:
a) Ví dụ: Tìm BC(6;9).
B(6) = {0; 6; 12; 18; 24; 30; 36; .... }
B(9) = {0; 9; 18; 27; 36; 45; ....... }
Vậy: BC(6;9) = {0; 18; 36; ........ }
Số nhỏ nhất khác 0 trong tập hợp
BC(6;9)là 18. Ta nói 18 là bội chung nhỏ
nhất của 6 và 9.
- Kí hiệu: BCNN(6;9) = 18
b) Khái niệm: BCNN của 2 hay nhiều số
là số nhỏ nhất khác 0 trong tập hợp bội
chung của các số đó.
- Nhận xét: Tất cả các BC(6;9) đều là bội
của BCNN(6;9).
* Chú ý:
BCNN(a;1) = a
BCNN của nhiều số mà có một số bằng
1.
VD: BCNN(5;1) = 5
BCNN(4;6;1) = BCNN(4;6)
GV: Để tìm BCNN của hai hay nhiều số
ta tìm tập hợp các BC của hai hay nhiều
số. Số nhỏ nhất khác 0 chính là BCNN.
Vậy còn cách nào tìm BCNN mà không
cần liệt kê như vậy? và cách tìm BCNN
có gì khác với cách tìm ƯCLN?
Hoạt động 2: Cách tìm BCNN
GV: Đưa ra ví dụ.
GV: Trước hết hãy phân tích các số 42;
70; 180 ra thừa số nguyên tố?
GV: Hãy chọn các thừa số nguyên tố
chung và riêng?
GV: Hãy lập tích các thừa số nguyên tố
vừa chọn, mỗi thừa số lấy với số mũ lớn
nhất?
GV: Giới thiệu tích đó là BCNN phải
tìm.
GV: Yêu cầu HS hoạt động nhóm:
- Rút ra quy tắc tìm BCNN.
- So sánh điểm giống và khác với tìm
ƯCLN.
Hoạt động 3: Hoạt động nhóm tìm
BCNN
GV: Cho HS đọc đề bài.
GV: Bài toán yêu cầu gì?
GV: Để tìm BCNN của hai hay nhiều số
ta tiến hành mấy bước? Đó là những
bước nào?
GV: Cho HS lên bảng trình bày.
GV: Cho HS nhận xét cách trình bày của
bạn.
GV: Uốn nắn và thống nhất cách trình
bày cho HS
GV: Cho HS nêu chú ý .
GV: Trong các số (12;16;48) thì 48 là gì
của 12 và 16?
BCNN(a;b;1) = BCNN(a;b)
2. Tìm BCNN bằng cách phân tích các số
ra thừa số nguyên tố
a) Ví dụ: Tìm BCNN(42;70;180).
42 = 2.3.7
70 = 2.5.7
180 = 22.32.5
BCNN(42;70;180) = 22.32.5.7
b) Cách tìm: (SGK)
?1 Hướng dẫn
* 8 = 23
12 = 22.3
BCNN(8;12) = 23.3 = 24
* 5 = 5; 7 = 7; 8 = 23
BCNN(5;7;8) = 23.5.7 = 280
* 12 = 22.3 ; 16 = 24
48 = 24.3
BCNN(12;16;48) = 24.3 = 48
* Chú ý: SGK-58
4.Củng cố -Luyện tập:
– GV nhấn mạnh lại KN BCNN- Cách tìm BCNN.
– Hướng dẫn HS làm các bài tập 150 SGK
5. Hướng dẫn học sinh học ở nhà:
– Học sinh về nhà học bài và làm các bài tập 149; 152 SGK.
- Hướng dẫn học sinh làm bài tập: Cần phân biệt rõ sự giống
và khác nhau trong tìm ƯCLN và BCNN.
– Chuẩn bị bài tập phần luyện tập.
có thể bạn quan tâm
TOÁN LỚP 6 BỘI CHUNG NHỎ NHẤT TIẾT 2
2
579
347
Giáo án, bài giảng lớp 6
2
(New)
TOÁN LỚP 6 ƯỚC CHUNG LỚN NHẤT TIẾT 2
2
622
278
Giáo án, bài giảng lớp 6
2
(New)
TOÁN LỚP 6 ƯỚC CHUNG LỚN NHẤT TIẾT 1
3
517
264
Giáo án, bài giảng lớp 6
3
(New)
Trình bày chi tiết về bài toán lựa chọn đơn vị trong tổng hợp ghép nối...
69
809
361
Kỹ thuật
69
(New)
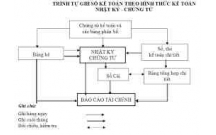
Hạch toán kế toán theo Hình thức kế toán - Nhật ký chứng từ
2
819
300
Kế toán, kiểm toán
2
(New)
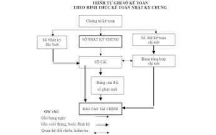
Thế nào là Hình thức kế toán Nhật ký chung?
2
625
300
Kế toán, kiểm toán
2
(New)
Tóm tắt lý thuyết và Giải bài tập Toán 6: Bội chung nhỏ nhất
4
659
286
Giải bài tập các môn
4
(New)
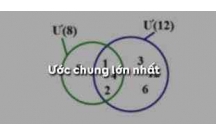
Tóm tắt kiến thức và Giải bài tập Toán lớp 6: Ước chung lớn nhất
5
557
292
Giải bài tập các môn
5
(New)
thông tin tài liệu
TOÁN LỚP 6 BỘI CHUNG NHỎ NHẤT
- 1. Bội chung nhỏ nhất:
a) Ví dụ: Tìm BC(6;9).
B(6) = {0; 6; 12; 18; 24; 30; 36; .... }
B(9) = {0; 9; 18; 27; 36; 45; ....... }
Vậy: BC(6;9) = {0; 18; 36; ........ }
Khái niệm: BCNN của 2 hay nhiều số là số nhỏ nhất khác 0 trong tập hợp bội chung của các số đó.
2. Tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố
Mở rộng để xem thêm
từ khóa liên quan
tài liệu mới trong mục này
tài liệu hot trong mục này
tài liệu giúp tôi
Nếu bạn không tìm thấy tài liệu mình cần có thể gửi yêu cầu ở đây để chúng tôi tìm giúp bạn!
×
