
Home
Giáo dục đào tạo
Giải bài tập các môn
Tóm tắt kiến thức và Giải bài Toán 6: Ôn tập và bổ túc về số tự nhiên
Tóm tắt kiến thức và Giải bài Toán 6: Ôn tập và bổ túc về số tự nhiên
Tóm t t ki n th c và Gi i bài Toán 6: Ôn t p và b túc v s tắ ế ứ ả ậ ổ ề ố ự
nhiên
A. Tóm t t ki n th c phép tr và phép chia:ắ ế ứ ừ
1. Cho hai s t nhiên a và b. N u có s t nhiên x mà b + x = a thì ta có phép tr a – bố ự ế ố ự ừ
= x. S a g i là s b tr , s b là s tr , s x là hi u s .ố ọ ố ị ừ ố ố ừ ố ệ ố
L u ý:ư
– N u b + x = a thì x = a – b và b = a – x.ế
– N u x = a – b thì b + x = a và b = a – x.ế
– Đi u ki n đ th c hi n đ c phép tr là s b tr ph i l n h n hay b ng s tr .ề ệ ể ự ệ ượ ừ ố ị ừ ả ớ ơ ằ ố ừ
2. Cho hai s t nhiên a và b, v i b ≠ 0. N u có s t nhiên x mà b . x = a thì ta có phépố ự ớ ế ố ự
chia h t a : b = x. S a g i là s b chia, s b là s chia, s x là th ng.ế ố ọ ố ị ố ố ố ươ
L u ý:ư
– N u b . x = a thì x = a : b n u b ≠ 0 và b = a : x n u x ≠ 0.ế ế ế
– N u x = a : b thì b . x = a và n u a ≠ 0 thì b = a : x.ế ế
3. Cho hai s t nhiên a và b, v i b ≠ 0, ta luôn tìm đ c hai s t nhiên q và r sao cho aố ự ớ ượ ố ự
= bq + r, trong đó 0 ≤ r < b.
Khi r ≠ 0 ta nói r ng ta có phép chia có d v i a là s b chia, b là s chia, q là th ng, rằ ư ớ ố ị ố ươ
là s d .ố ư
4. S chia bao gi cũng khác 0.ố ờ
B. Gi i bài t p trong sách giáo khoa Trang 22, 23, 24 Toán Đ i s l p 6 t p 1ả ậ ạ ố ớ ậ
Bài 1. (Trang 22 SGK Toán 6 t p 1)ậ
Hà N i, Hu , Nha Trang, Thành ph H Chí Minh n m trên qu c l 1 theo th t nhộ ế ố ồ ằ ố ộ ứ ự ư
trên. Cho bi t các quãng đ ng trên qu c l y:ế ườ ố ộ ấ
Hà N i – Hu : 658km,ộ ế
Hà N i – Nha Trang: 1278km,ộ
Hà N i – Thành ph H Chí Minh: 1710km.ộ ố ồ
Tính các quãng đ ng: Hu – Nha Trang, Nha Trang – Thành ph H Chí Minh.ườ ế ố ồ
Đáp án và bài gi i:ả
Quãng đ ng Hu – Nha Trang: 1278 – 658 = 620 (km).ườ ế
Nha Trang – Thành ph H Chí Minh: 1710 – 1278 = 432 (km).ố ồ
Bài 2. (Trang 23 SGK Toán 6 t p 1)ậ
Các s li u v kênh đào Xuy-ê (Ai C p) n i Đ a Trung H i và H ng H i đ c choố ệ ề ậ ố ị ả ồ ả ượ
trong b ng 1 và b ng 2.ả ả
B ng 1ả
Kênh đào Xuy-ê Năm 1869 Năm 1955
Chi u r ng m t kênhề ộ ặ 58m 135m
Chi u r ng đáy kênhề ộ 22m 50m
Đ sâu c a kênhộ ủ 6m 13m
Th i gian tàu qua kênhờ48 giờ14 giờ
B ng 2ả
Hành trình Qua mũi H o V ngả ọ Qua kênh Xuy-ê
Luân Đôn - Bom-bay 17400km 10100km
Mác-xây- Bom-bay 16000km 7400km
Ô-đét-xa- Bom-bay 19000km 6800km
a) Trong b ng 1, các s li u năm 1955 tăng thêm (hay gi m b t) bao nhiêu so v iả ố ệ ở ả ớ ớ
năm 1869 (năm khánh thành kênh đào)?
b) Nh đi qua kênh đào Xuy-ê, m i hành trình trong b ng 2 gi m b t đ c bao nhiêuờ ỗ ả ả ớ ượ
kilômét?
Đáp án và bài gi i:ả
Chi u r ng m t kênh tăng lên 77m.ề ộ ặ
Chi u r ng đáy kênh tăng lên 28m.ề ộ
Đ sâu c a kênh tăng lên 7m.ộ ủ
Th i gian tàu qua kênh gi m b t 34 gi .ờ ả ớ ờ
Hành trình Luân Đôn – Bom-bay gi m b t 7300km.ả ớ
Hành trình Mác-xây – Bom-bay gi m b t 8600km.ả ớ
Hành trình Ô-đét-xa – Bom-bay gi m b t 12200km.ả ớ
Kênh đào Xuy-ê Năm 1869 Năm 1955
Chi u r ng m t kênhề ộ ặ 58m 135m
Chi u r ng đáy kênhề ộ 22m 50m
Đ sâu c a kênhộ ủ 6m 13m
Th i gian tàu qua kênhờ48 giờ14 giờ
Bài 3. (Trang 23 SGK Toán 6 t p 1)ậ
Tính kh i l ng c a qu bí hình 18 khi cân thăng b ng:ố ượ ủ ả ở ằ
Bài gi i:ả
V n d ng đi u l u ý trong ph n tóm t t ki n th c.ậ ụ ề ư ầ ắ ế ứ
Theo hình v : Kh i l ng qu bí + 100g = 1500g. Do đó kh i l ng c a qu bí làẽ ố ượ ả ố ượ ủ ả
1500g – 100g = 1400g.
Bài 4. (Trang 24 SGK Toán 6 t p 1)ậ
Tìm s t nhiên x, bi t:ố ự ế
a) x : 13 = 41; b) 1428 : x = 14; c) 4x : 17 = 0;
d) 7x – 8 = 713; e) 8(x – 3) = 0; g) 0 : x = 0.
Đáp án và h ng d n gi i bài 44:ướ ẫ ả
V n d ng đi u l u ý trong ph n tóm t t ki n th c.ậ ụ ề ư ầ ắ ế ứ
a) N u x : 13 = 41 thì x = 41 . 13 = 533.ế
b) N u 1428 : x = 14 thì x = 1428 : 14 = 102.ế
c) N u 4x : 17 = 0 thì x = 0.ế
d) 7x – 8 = 713 thì 7x = 713 + 8 = 721. Do đó x = 721 : 7 = 103.
e) N u 8(x – 3) = 0 thì x – 3 = 0. Do đó x = 3.ế
g) Vì x là s chia nên x ≠ 0. T 0 : x = 0 suy ra x . 0 = 0. Vì m i s nhân v i 0 đ u b ngố ừ ọ ố ớ ề ằ
0 nên x là m t s t nhiên b t kì, khác 0.ộ ố ự ấ
Bài 5. (Trang 24 SGK Toán 6 t p 1)ậ
Đi n vào ô tr ng sao cho a = b.q + r v i 0 ≤ r < b:ề ố ớ
Đáp án:
a 392 278 357 b 420
b 28 13 21 14 35
q 14 21 17 25 12
r 0 5 0 10 0
Bài 6. (Trang 24 SGK Toán 6 t p 1)ậ
a) Trong phép chia cho 2, s d có th b ng 0 ho c 1. Trong m i phép chia cho 3, choố ư ể ằ ặ ỗ
4, cho 5, s d có th b ng bao nhiêu?ố ư ể ằ
b) D ng t ng quát c a s chia h t cho 2 là 2k, d ng t ng quát c a s chia h t cho 2 dạ ổ ủ ố ế ạ ổ ủ ố ế ư
1 là 2k + 1 v i k N. Hãy vi t d ng t ng quát c a s chia h t cho 3, s chia h t cho 3ớ ∈ ế ạ ổ ủ ố ế ố ế
d 1, s chia h t cho 3 d 2.ư ố ế ư
Đáp án và h ng d n gi i bài 46:ướ ẫ ả
a) S d trong phép chia m t s t nhiên cho s t nhiên b ≠ 0 là m t s t nhiên r < bố ư ộ ố ự ố ự ộ ố ự
nghĩa là r có th là 0; 1;…; b – 1.ể
S d trong phép chia cho 3 có th là 0; 1; 2.ố ư ể
S d trong phép chia cho 4 có th là: 0; 1; 2; 3.ố ư ể
S d trong phép chia cho 5 có th là: 0; 1; 2; 3; 4.ố ư ể
b) D ng t ng quát c a s t nhiên chia h t cho 3 là 3k, v i k N.ạ ổ ủ ố ự ế ớ ∈
D ng t ng quát c a s t nhiên chia h t cho 3, d 1 là 3k + 1, v i k N.ạ ổ ủ ố ự ế ư ớ ∈
D ng t ng quát c a s t nhiên chia h t cho 3, d 2 là 3k + 2, v i k N.ạ ổ ủ ố ự ế ư ớ ∈
Bài 7. (Trang 24 SGK Toán 6 t p 1)ậ
Tìm s t nhiên x, bi tố ự ế
a) (x – 35) – 120 = 0;
b) 124 + (118 – x) = 217;
c) 156 – (x + 61) = 82.
Đáp án và h ng d n gi i:ướ ẫ ả
a) (x-35) -120 = 0
x-35 = 0 +120
x-35 = 120
x = 120 +35
x = 155
b) 124 + (118 -x) = 217
118 – x = 217-124
118 – x = 93
x = 118 – 93
x = 25
c) 156 -(x + 61) = 82
x + 61 = 156 -82
x + 61 = 74
x = 74- 61
x = 13
Bài 8. (Trang 24 SGK Toán 6 t p 1)ậ
Tính nh m b ng cách thêm vào s h ng này, b t đi s h ng kia cùng m t s thíchẩ ằ ở ố ạ ớ ở ố ạ ộ ố
h p:ợ
Ví d : 57 + 96 = (57 – 4) + (96 + 4) = 53 + 100 = 153.ụ
Hãy tính nh m: 35 + 98; 46 + 29.ẩ
Đáp án và h ng d n gi i:ướ ẫ ả
35 + 98 = (35 – 2) + (98 + 2) = 33 + 100 = 133.
46 + 29 = (46 – 1) + (29 + 1) = 45 + 30 = 75.
Bài 9. (Trang 24 SGK Toán 6 t p 1)ậ
Tính nh m b ng cách thêm vào s b tr và s tr cùng m t s thích h p:ẩ ằ ố ị ừ ố ừ ộ ố ợ
Ví d : 135 – 98 = (135 + 2) – (98 + 2) = 137 – 100 = 37.ụ
Hãy tính nh m: 321 – 96; 1354 – 997.ẩ
Đáp án và h ng d n gi i:ướ ẫ ả
321 – 96 = (321 + 4) – (96 + 4) = 325 -100 = 225.
1354 – 997 = (1354 + 3) – (997 + 3) = 1357 – 1000 = 357.
Bài 10. (Trang 24 SGK Toán 6 t p 1)ậ
S d ng máy tính b túi:đ tính:ử ụ ỏ ể
425 – 257; 91 – 56; 82 – 56; 73 – 56; 652 – 46 – 46 – 46.
H c sinh t th c hànhọ ự ự
có thể bạn quan tâm

Tóm tắt kiến thức và Giải bài tập Toán lớp 6: Ghi số tự nhiên
3
689
371
Giải bài tập các môn
3
(New)

Tóm tắt kiến thức và Giải bài tập Toán lớp 6: Lý thuyết lũy thừa với s...
6
823
367
Giải bài tập các môn
6
(New)

Hướng dẫn giải bài tập môn Toán lớp 5: Chia một số tự nhiên cho một số...
4
759
343
Giải bài tập các môn
4
(New)

Hệ thống kiến thức cơ bản và giải bài tập Toán lớp 8: Chia đa thức cho...
2
879
433
Tài liệu, đề thi môn Toán
2
(New)

Tóm tắt kiến thức và Giải bài tập Toán lớp 6: Thứ tự thực hiện các phé...
5
951
359
Giải bài tập các môn
5
(New)

Tóm tắt kiến thức và giải bài tập Toán lớp 8: Chia đa thức một biến đã...
5
866
836
Tài liệu, đề thi môn Toán
5
(New)
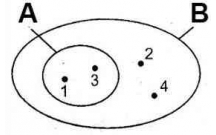
Tóm tắt kiến thức và giải bài tập Toán lớp 6: Tập hợp, Phần tử của tập...
2
581
288
Giải bài tập các môn
2
(New)

Tóm tắt kiến thức và Giải bài tập Toán lớp 6: Tập hợp các số nguyên
3
630
345
Giải bài tập các môn
3
(New)
thông tin tài liệu
A. Tóm tắt kiến thức phép trừ và phép chia:
1. Cho hai số tự nhiên a và b. Nếu có số tự nhiên x mà b + x = a thì ta có phép trừ a – b = x. Số a gọi là số bị trừ, số b là số trừ, số x là hiệu số.
Lưu ý:
– Nếu b + x = a thì x = a – b và b = a – x.
– Nếu x = a – b thì b + x = a và b = a – x.
– Điều kiện để thực hiện được phép trừ là số bị trừ phải lớn hơn hay bằng số trừ.
2. Cho hai số tự nhiên a và b, với b ≠ 0. Nếu có số tự nhiên x mà b . x = a thì ta có phép chia hết a : b = x. Số a gọi là số bị chia, số b là số chia, số x là thương.
Lưu ý:
– Nếu b . x = a thì x = a : b nếu b ≠ 0 và b = a : x nếu x ≠ 0.
– Nếu x = a : b thì b . x = a và nếu a ≠ 0 thì b = a : x.
3. Cho hai số tự nhiên a và b, với b ≠ 0, ta luôn tìm được hai số tự nhiên q và r sao cho a = bq + r, trong đó 0 ≤ r < b.
Khi r ≠ 0 ta nói rằng ta có phép chia có dư với a là số bị chia, b là số chia, q là thương, r là số dư.
4. Số chia bao giờ cũng khác 0.
.....
Mở rộng để xem thêm
tài liệu mới trong mục này
tài liệu hot trong mục này
tài liệu giúp tôi
Nếu bạn không tìm thấy tài liệu mình cần có thể gửi yêu cầu ở đây để chúng tôi tìm giúp bạn!
xem nhiều trong tuần
Địa lý 12 Phát triển cây công nghiệp lâu năm Tây Nguyên
Đề thi và lời giải môn xác suất thống kê của trường Học viện ngân hàng
Giáo trình Quản trị học của Đại học kinh tế quốc dân
MẪU GIẤY THI A4
MẪU GIỚI THIỆU CHUYỂN SINH HOẠT HỘI
Bài tập ôn tập cuối tuần lớp 2: Tuần 31
yêu cầu tài liệu
Giúp bạn tìm tài liệu chưa có
×



