Home
Giáo dục đào tạo
Tài liệu, đề thi môn Toán
Tổng hợp một số đề thi học sinh giỏi toán dành cho học sinh lớp 6
Tổng hợp một số đề thi học sinh giỏi toán dành cho học sinh lớp 6
Đề số 1
Thời gian làm bài 120 phút
Câu 1 : (2 điểm) Cho biểu thức
122
12
23
23
aaa
aa
A
a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là
một phân số tối giản.
Câu 2: (1 điểm)
Tìm tất cả các số tự nhiên có 3 chữ số
abc
sao cho
1
2
nabc
và
2
)2( ncba
Câu 3: (2 điểm)
a. Tìm n để n2 + 2006 là một số chính phương
b. Cho n là số nguyên tố lớn hơn 3. Hỏi n2 + 2006 là số nguyên tố hay là hợp số.
Câu 4: (2 điểm)
a. Cho a, b, n N* Hãy so sánh
nb
na
và
b
a
b. Cho A =
110
110
12
11
; B =
110
110
11
10
. So sánh A và B.
Câu 5: (2 điểm)
Cho 10 số tự nhiên bất kỳ : a1, a2, ....., a10. Chứng minh rằng thế nào cũng có một
số hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.
Câu 6: (1 điểm)
Cho 2006 đường thẳng trong đó bất kì 2 đườngthẳng nào cũng cắt nhau. Không có 3
đường thẳng nào đồng qui. Tính số giao điểm của chúng.
Đề số 2
Thời gian làm bài 120 phút
Câu1:
a. Tìm các số tự nhiên x, y. sao cho (2x + 1)(y – 5) = 12
b.Tìm số tự nhiên sao cho 4n-5 chia hết cho 2n-1
c. Tìm tất cả các số B =
62xy427
, biết rằng số B chia hết cho 99
Câu 2.
a. chứng tỏ rằng
230
112
n
n
là phân số tối giản.
b. Chứng minh rằng :
2
2
1
+
2
3
1
+
2
4
1
+...+
2
100
1
<1
Câu 3:
Một bác nông dân mang cam đi bán. Lần thứ nhất bán 1/2số cam và 1/2 quả; Lần thứ 2
bán 1/3 số cam còn lạivà 1/3 quả ; Lần thứ 3 bán 1/4số cam còn lại và 3/4 quả. Cuối
cung còn lại 24 quả . Hỏi số cam bác nông dân đã mang đi bán .
Câu 4:
Cho 101 đường thẳng trong đó bất cứ hai đường thẳng nào cũng cắt nhau, không có
ba đường thẳng nào đồng quy. Tính số giao điểm của chúng.
Đề số 3
Thời gian làm bài: 120’
Bài 1:(1,5đ)
Tìm x
a) 5x = 125; b) 32x = 81 ; c) 52x-3 – 2.52 = 52.3
Bài 2: (1,5đ)
Cho a là số nguyên. Chứng minh rằng:
a
5 5 5a
Bài 3: (1,5đ)
Cho a là một số nguyên. Chứng minh rằng:
a. Nếu a dương thì số liền sau a cũng dương.
b. Nếu a âm thì số liền trước a cũng âm.
c. Có thể kết luận gì về số liền trước của một số dương và số liền sau của một số âm?
Bài 4: (2đ)
Cho 31 số nguyên trong đó tổng của 5 số bất kỳ là một số dương. Chứng minh rằng
tổng của 31 số đó là số dương.
Bài 5: (2đ)
Cho các số tự nhiên từ 1 đến 11 được viết theo thứ tự tuỳ ý sau đó đem cộng mỗi số
với số chỉ thứ tự của nó ta được một tổng. Chứng minh rằng trong các tổng nhận được,
bao giờ cũng tìm ra hai tổng mà hiệu của chúng là một số chia hết cho 10.
Bài 6: (1,5đ)
Cho tia Ox. Trên hai nữa mặt phẳng đối nhău có bờ là Ox. Vẽ hai tia Oy và Oz sao
cho góc xOy và xOz bắng 1200. Chứng minh rằng:
a.
xOy xOz yOz
b. Tia đối của mỗi tia Ox, Oy, Oz là phân giác của góc hợp bởi hai tia còn lại.
Đề số 4
Thời gian làm bài 120 phút
Câu 1. Tính:
a. A = 4 + 2 2 + 2 3 + 2 4 +. . . + 2 20
b. tìm x biết: ( x + 1) + ( x + 2) + . . . + ( x + 100) = 5750.
Câu 2.
a. Chứng minh rằng nếu:
egcdab
11 thì
degabc
11.
b. Chứng minh rằng: 10 28 + 8
72.
Câu 3.
Hai lớp 6A; 6B cùng thu nhặt một số giấy vụn bằng nhau. Lớp 6A có 1 bạn thu được
26 kg còn lại mỗi bạn thu được 11 kg ; Lớp 6B có 1 bạn thu được 25 kg còn lại mỗi bạn
thu được 10kg . Tính số học sinh mỗi lớp biết rằng số giấy mỗi lớp thu được trong
khoảng 200kg đến 300kg.
Câu 4.
Tìm 3 số có tổng bằng 210, biết rằng
7
6
số thứ nhất bằng
11
9
số thứ 2 và bằng
3
2
số thứ
3.
Câu 5. Bốn điểm A,B,C,Dkhông nằm trên đường thẳng a. Chứng tỏ rằng đường thẳng a
hoặc không cắt, hoặc cắt ba, hoặc cắt bốn đoạn thẳng AB, AC, AD, BC, BD, CD.
Đề số 5
Thời gian làm bài 120 phút
Bài 1 (3đ):
a) So sánh: 222333 và 333222
b) Tìm các chữ số x và y để số
281 yx
chia hết cho 36
c) Tìm số tự nhiên a biết 1960 và 2002 chia cho a có cùng số dư là 28
Bài 2 (2đ):
Cho : S = 30 + 32 + 34 + 36 + ... + 32002
a) Tính S
b) Chứng minh S
7
Bài 3 (2đ):
Tìm số tự nhiên nhỏ nhất, biết rằng khi chia số này cho 29 dư 5 và chia cho 31 dư 28
Bài 4 (3đ):
Cho góc AOB = 1350. C là một điểm nằm trong góc AOB biết góc BOC = 900
a) Tính góc AOC
b) Gọi OD là tia đối của tia OC. So sánh hai góc AOD và BOD
Đề số 6
Thời gian làm bài 120 phút
Bài 1( 8 điểm )
1. Tìm chữ số tận cùng của các số sau:
a) 571999 b) 931999
2. Cho A= 9999931999 - 5555571997. Chứng minh rằng A chia hết cho 5.
3 . Cho phân số
b
a
( a<b) cùng thêm m đơn vị vào tử và mẫu thì phân số mới lớn hơn
hay bé hơn
b
a
?
4. Cho số
16*4*710*155
có 12 chữ số . chứng minh rằng nếu thay các dấu * bởi các
chưc số khác nhau trong ba chữ số 1,2,3 một cách tuỳ thì số đó luôn chia hết cho 396.
5. chứng minh rằng:
a)
3
1
64
1
32
1
16
1
8
1
4
1
2
1
; b)
16
3
3
100
3
99
...
3
4
3
3
3
2
3
1
10099432
Bài 2: (2 điểm )
Trên tia Ox xác định các điểm A và B sao cho OA = a(cm), OB = b (cm)
a) Tính độ dài đoạn thẳng AB, biết b< a
b) Xác định điểm M trên tia Ox sao cho OM =
2
1
(a+b).
Đề số 7
Thời gian làm bài: 120 phút.
A – Phần số học : (7 điểm )
Câu 1: (2điểm)
a) Các phân số sau có bằng nhau không? Vì sao?
99
23
;
99999999
23232323
;
9999
2323
;
999999
232323
b) Chứng tỏ rằng: 2x + 3y chia hết cho 17
9x + 5y chia hết cho 17
Câu 2: (2điểm)
Tính giá trị của biểu thức sau:
A = (
7
1
+
23
1
-
1009
1
):(
23
1
+
7
1
-
1009
1
+
7
1
.
23
1
.
1009
1
) + 1:(30. 1009 – 160)
Câu 3: (2điểm)
a) Tìm số tự nhiên x , biết : (
3.2.1
1
+
4.3.2
1
+ . . . +
10.9.8
1
).x =
45
23
b) Tìm các số a, b, c , d
N , biết :
43
30
=
d
c
b
a
1
1
1
1
Câu 4 : (1điểm)
Một số tự nhiên chia cho 120 dư 58, chia cho 135 dư 88. Tìm a, biết a bé nhất.
B – Phần hình học (3 điểm) :
Câu 1: ( 2 điểm )
Góc tạo bởi 2 tia phân giác của 2 góc kề bù, bằng bao nhiêu? Vì sao?
Câu 2: ( 1 điểm)
Cho 20 điểm, trong đó có a điểm thẳng hàng. Cứ 2 điểm, ta vẽ một đường thẳng. Tìm a ,
biết vẽ được tất cả 170 đường thẳng.
Đề số 8
Thời gian làm bài : 120’
Bài 1 : (3 đ)
Người ta viết các số tự nhiên liên tiếp bắt đầu từ 1 đến 2006 liền nhau thành một số
tự nhiên L . Hỏi số tự nhiên L có bao nhiêu chữ số .
Bài 2 : (3đ)
Có bao nhiêu chữ số gồm 3 chữ số trong đó có chữ số 4 ?
Bài 3 : (4đ)
Cho băng ô gồm 2007 ô như sau :
17 36 19
Phần đầu của băng ô như trên . Hãy điền số vào chố trống sao cho tổng 4 số ở 4 ô liền
nhau bằng 100 và tính :
a) Tổng các số trên băng ô .
b) Tổng các chữ số trên băng ô .
c) Số điền ở ô thứ 1964 là số nào ?
Đề số 9
Thời gian làm bài: 120 phút
Bài 1:(1,5đ) Tìm x, biết:
a) 5x = 125; b) 32x = 81 ; c) 52x-3 – 2.52 = 52.3
Bài 2 :(1,5đ) Cho a là số nguyên. Chứng minh rằng:
a
5 5 5a
Bài 3: (1,5đ) Cho a là một số nguyên. Chứng minh rằng:
a) Nếu a dương thì số liền sau a cũng dương.
b) Nếu a âm thì số liền trước a cũng âm.
c) Có thể kết luận gì về số liền trước của một số dương và số liền sau của một số âm?
Bài 4: (2đ) Cho 31 số nguyên trong đó tổng của 5 số bất kỳ là một số dương. Chứng
minh rằng tổng của 31 số đó là số dương.
Bài 5: (2đ). Cho các số tự nhiên từ 1 đến 11 được viết theo thứ tự tuỳ ý sau đó đem
cộng mỗi số với số chỉ thứ tự của nó ta được một tổng. Chứng minh rằng trong các tổng
nhận được, bao giờ cũng tìm ra hai tổng mà hiệu của chúng là một số chia hết cho 10.
Bài 6: (1,5đ) Cho tia Ox. Trên hai nữa mặt phẳng đối nhau có bờ là Ox. Vẽ hai tia Oy
và Oz sao cho góc xOy và xOz bắng 1200. Chứng minh rằng:
a)
xOy xOz yOz
b) Tia đối của mỗi tia Ox, Oy, Oz là phân giác của góc hợp bởi hai tia còn lại.
Đề số 10
Thời gian làm bài: 120 phút
Câu 1:
a) Chứng tỏ rằng số:
1995
10 8
9
là một số tự nhiên.
b) Tìm 2 số tự nhiên có tổng bằng 432 và ƯCLN của chúng là 36.
Câu 2: Tính nhanh:
a) 35.34 + 35.86 + 65.75 + 65.45 ; b) 21.72 - 11.72 + 90.72 + 49.125.16 ;
Câu 3: So sánh: 920 và 2713
Câu 4: Tìm x biết: a) |2x - 1| = 5 ; b) ( 5x - 1).3 - 2 = 70
Câu 5: Chứng minh tổng sau chia hết cho 7.
A = 21 + 22 + 23 + 24 +...+ 259 + 260 ;
Câu 6:
Để chuẩn bị cho kỳ thi học sinh giỏi, một học sinh giải 35 bài toán. Biết rằng cứ mỗi bài
đạt loại giỏi được thưởng 20 điểm, mỗi bài đạt loại khá, trung bình được thưởng 5 điểm.
Còn lại mỗi bài yếu, kém bị trừ 10 điểm. Làm xong 35 bài em đó được thưởng 130
điểm. Hỏi có bao nhiêu bài loại giỏi, bao nhiêu bài loại yếu, kém. Biết rằng có 8 bài
khá và trung bình.
Câu 7: Cho 20 điểm trong đó không có 3 điểm nào thẳng hàng, cứ 2 điểm ta sẽ vẽ một
đường thẳng. Có tất cả bao nhiêu đường thẳng.
Đề số 11
Thời gian làm bài: 120 phút
I. Trắc ngiệm: Điền dấu x vào ô thích hợp:( 1 điểm)
Câu Đúng Sai
a. Số -5
5
1
bằng –5 +
5
1
b. Số 11
7
3
bằng
7
80
c. Số -11
4
5
bằng –11-
4
5
d. Tổng -3
5
1
+ 2
3
2
bằng -1
15
13
II. Tự luận:
Câu 1: Thực hiện các phép tính sau: (4 điểm)
a)
729.7239.162.54.18234.9.3
27.81.243729.2181
22
b.
100.99
1
99.98
1
4.3
1
3.2
1
2.1
1
c.
1
100
1
4
1
3
1
2
1
2222
d.
629199
920915
27.2.76.2.5
8.3.494.5
Câu 2: (2 điểm) Một quãng đường AB trong 4 giờ. Giờ đầu đi được
3
1
quãng đường AB. Giờ thứ 2 đi
kém giờ đầu là
12
1
quãng đường AB, giờ thứ 3 đI kém giờ thứ 2
12
1
quãng đường AB. Hỏi giờ thứ
tư đi mấy quãng đường AB?
Câu 3: (2 điểm)
a. Vẽ tam giác ABC biết BC = 5 cm; AB = 3cm ;AC = 4cm.
b. Lấy điểm 0 ở trong tam giác ABC nói trên.Vẽ tia A0 cắt BC tại H, tia B0 cắt AC tại I,tia C0 cắt AB
tại K. Trong hình đó có có bao nhiêu tam giác.
Câu 4: (1 điểm)
a. Tìm hai chữ số tận cùng của các số sau: 2100; 71991
b.Tìm bốn chữ số tận cùng của số sau: 51992
Đề số 12
Thời gian làm bài: 120 phút
Bài 1( 8 điểm )
1. Tìm chữ số tận cùng của các số sau:
a) 571999 b) 931999
2. Cho A= 9999931999 - 5555571997. Chứng minh rằng A chia hết cho 5.
3 . Cho phân số
b
a
( a<b) cùng thêm m đơn vị vào tử và mẫu thì phân số mới lớn hơn hay bé hơn
b
a
?
4. Cho số
16*4*710*155
có 12 chữ số . chứng minh rằng nếu thay các dấu * bởi các chưc số khác
nhau trong ba chữ số 1,2,3 một cách tuỳ thì số đó luôn chia hết cho 396.
5. Chứng minh rằng:
a)
3
1
64
1
32
1
16
1
8
1
4
1
2
1
b)
16
3
3
100
3
99
...
3
4
3
3
3
2
3
1
10099432
Bài 2( 2 điểm )
Trên tia Ox xác định các điểm A và B sao cho OA= a(cm), OB=b (cm)
a) Tính độ dài đoạn thẳng AB, biết b< a
b) Xác định điểm M trên tia Ox sao cho OM =
2
1
(a+b).
Đề số 13
Thời gian làm bài: 120 phút (không kể thời gian chép đề)
Bài 1 (3điểm)
a, Cho A = 9999931999 - 5555571997. Chứng minh rằng A chia hết cho 5
b, Chứng tỏ rằng:
41
1
+
42
1
+
43
1
+ …+
79
1
+
80
1
>
12
7
Bài 2 (2,5điểm)
Tổng số trang của 8 quyển vở loại 1 ; 9 quyển vở loại 2 và 5 quyển vở loại 3 là 1980
trang. Số trang của một quyển vở loại 2 chỉ bằng
3
2
số trang của 1 quyển vở loại 1. Số
trang của 4 quyển vở loại 3 bằng số trang của 3 quyển vở loại 2. Tính số trang của mỗi
quyển vở mỗi loại.
Bài 3: (2điểm).
Tìm số tự nhiên n và chữ số a biết rằng:
1+ 2+ 3+ …….+ n =
aaa
có thể bạn quan tâm
HỆ THỐNG CÁC BÀI TẬP ÔN TẬP DÀNH CHO HỌC SINH GIỎI TOÁN LỚP 2
16
1.461
420
Tài liệu, đề thi học sinh giỏi
16
(New)
BÀI TẬP DÀNH CHO HỌC SINH GIỎI MÔN TOÁN - LỚP 2 CHUYÊN ĐỀ PHÉP NHÂN
1
2.788
484
Tài liệu, đề thi môn Toán
1
(New)
Tuyển tập toán ôn luyện dành cho học sinh giỏi Toán lớp 2
4
1.635
392
Tài liệu, đề thi môn Toán
4
(New)
Đề thi môn tiếng anh lớp 9 dành cho học sinh giỏi 150'
23
4.126
375
Tiếng Anh phổ thông
23
(New)
Đề thi học sinh giỏi Vật lý Lớp 9 Kỳ thi HỌC SINH GIỎI CẤP THÀNH PHỐ H...
3
1.423
395
Tài liệu, đề thi học sinh giỏi
3
(New)
Tổng hợp các bài tập bồi dưỡng học sinh giỏi Hóa học lớp 8
8
1.030
576
Tài liệu, đề thi Hóa Học
8
(New)
LÝ THUYẾT SINH HỌC 12: SỰ PHÁT TRIỂN CỦA SINH GIỚI QUA CÁC ĐẠI ĐỊA CHẤ...
3
814
360
Tài liệu, đề thi Sinh Học
3
(New)
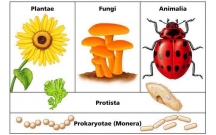
Tóm tắt lý thuyết và hướng dẫn giải bài tập Sinh 10: Các giới sinh vật
4
672
324
Giải bài tập các môn
4
(New)
thông tin tài liệu
Đề số 1
Thời gian làm bài 120 phút
Câu 1 : (2 điểm) Cho biểu thức
a, Rút gọn biểu thức
b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.
Câu 2: (1 điểm)
Tìm tất cả các số tự nhiên có 3 chữ số sao cho và
Câu 3: (2 điểm)
a. Tìm n để n2 + 2006 là một số chính phương
b. Cho n là số nguyên tố lớn hơn 3. Hỏi n2 + 2006 là số nguyên tố hay là hợp số.
Câu 4: (2 điểm)
a. Cho a, b, n N* Hãy so sánh và
b. Cho A = ; B = . So sánh A và B.
Mở rộng để xem thêm
tài liệu mới trong mục này
Giải bài tập trang 144 SGK Hóa lớp 9: Mối liên hệ giữa etilen, rượu etylic và axit axetic
Giải bài tập Hóa lớp 9: Rượu etylic
Giải bài tập Hóa lớp 9: Khái niệm về hợp chất hữu cơ và hoá học hữu cơ
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm giá trị phần trăm một số
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm tỉ số phần trăm của hai số
tài liệu hot trong mục này
Ôn tập kiến thức môn Toán lớp 2 chuyên đề: Phép cộng có nhớ
Bộ đề thi giữa học kì 1 môn Toán lớp 2 theo Thông tư 22
Một số dạng bài tập về Phép cộng, trừ các số nguyên trong chương trình Toán lớp 6
Bài tập ôn tập cuối tuần lớp 2: Tuần 21
Lý thuyết và một số dạng bài tập về Lũy thừa với số mũ tự nhiên và các phép toán (Toán lớp 6)
tài liệu giúp tôi
Nếu bạn không tìm thấy tài liệu mình cần có thể gửi yêu cầu ở đây để chúng tôi tìm giúp bạn!
×
