Home
Giáo dục đào tạo
Tài liệu, đề thi môn Toán
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng dụng đạo hàm - Mức độ 4 phần 1
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng dụng đạo hàm - Mức độ 4 phần 1
Câu 1: (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Cho hàm số
y f x
có đồ thị
y f x
như hình vẽ. Xét hàm số
3 2
1 3 3 2018
3 4 2
g x f x x x x
. Mệnh đề nào dưới đây đúng?
A.
3; 1
min 1g x g
.B.
3; 1
min 1g x g
C.
3; 1
min 3g x g
D.
3; 1
3 1
min 2
g g
g x
Lời giải
Chọn A
Ta có:
3 2 2
1 3 3 3 3
2018
3 4 2 2 2
g x f x x x x g x f x x x
Căn cứ vào đồ thị
y f x
, ta có:
1 2 1 0
1 1 1 0
3 3 3 0
f g
f g
f g
Ngoài ra, vẽ đồ thị
P
của hàm số
2
3 3
2 2
y x x
trên cùng hệ trục tọa độ như hình vẽ bên
(đường nét đứt ), ta thấy
P
đi qua các điểm
3;3
,
1; 2
,
1;1
với đỉnh
3 33
;
4 16
I
.
Rõ ràng
oTrên khoảng
1;1
thì
2
3 3
2 2
f x x x
, nên
0 1;1xg x
oTrên khoảng
3; 1
thì
2
3 3
2 2
f x x x
, nên
0 3; 1xg x
Ox
y
1
1
3
3
1
2
x
y
1
1
3
3
1
2
P
Từ những nhận định trên, ta có bảng biến thiên của hàm
4 4
2 2 2 6 2 6x x x x m
trên
3;1
như sau:
Vậy
3; 1
min 1g x g
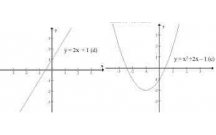
Câu 2: (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Có bao nhiêu giá trị
nguyên của tham số
m
để đường thẳng
4y m x
cắt đồ thị của hàm số
2 2
1 9y x x
tại bốn điểm phân biệt?
A.
1.
B.
5.
C.
3.
D.
7.
Lời giải
Chọn B
Ta có phương trình hoành độ giao điểm
2 2
1 9 4x x m x
2 2
1 9 1
4
x x m
x
,
4x
.
Số nghiệm của
1
bằng số giao điểm của 2 đồ thị hàm số
2 2
1 9
4
x x
y f x x
và
y m
.
Ta có:
2 2 2 2 4 3 2
2 2
2 9 4 2 1 4 9 1 3 16 10 80 9
4 4
x x x x x x x x x x x x
f x x x
4 3 2
0 3 16 10 80 9 0f x x x x x
Giải phương trình bằng MTBT ta được 4 nghiệm
1
2
3
4
2,169
0,114
2,45
4,94
x
x
x
x
. Các nghiệm này đã được lưu
chính xác ở trong bộ nhớ của MTBT.
Bảng biến thiên:
Từ BBT và
2; 1; 0;1;2 .m m
Câu 3: (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Hàm số
3 3 3
y x m x n x
(tham số
;m n
) đồng biến trên khoảng
;
. Giá trị nhỏ nhất
của biểu thức
2 2
4P m n m n
bằng
A.
16
.B.
4
.C.
1
16
.D.
1
4
.
_
Lời giải
Chọn C
Ta có
2 2 2 2 2 2
3 3 3 3 2y x m x n x x m n x m n
!
"
.
Hàm số đồng biến trên
;
00
0
amn
# # $
% $
.
TH1:
0
00
m
mn n
#
.
Do vai trò của
,m n
là như nhau nên ta chỉ cần xét trường hợp
0m
.
2
1 1 1
4 2 1
4 16 16
P n n n
&
.
TH2:
0 0; 0m n m n #
(do vai trò của
,m n
như nhau).
Ta có
2
2
1 1 1
2 4 2
4 16 16
P m n n
.
Từ
1 , 2
ta có
min
1
16
P
. Dấu
" "
xảy ra khi và chỉ khi
1; 0
8
m n
hoặc
1
0; 8
m n
.
Câu 4: (THPT Chuyên Hùng Vương-Phú Thọ-lần 1-NH2017-2018) Hình vẽ bên là đồ
thị của hàm số
y f x
.
Gọi
S
là tập hợp các giá trị nguyên dương của tham số
m
để hàm số
1y f x m
có
5
điểm cực trị. Tổng giá trị tất cả các phần tử của
S
bằng
A.
12
.B.
15
.C.
18
.D.
9
.
Lời giải
Chọn A
Nhận xét: Số giao điểm của
:C y f x
với
Ox
bằng số giao điểm của
: 1C y f x
với
Ox
.
Vì
0m
nên
: 1C y f x m
có được bằng cách tịnh tiến
: 1C y f x
lên trên
m
đơn vị.
Ox
y
2
3
4 4
2 2 2 6 2 6x x x x m
TH1:
0 3m
. Đồ thị hàm số có
7
điểm cực trị. Loại.
TH2:
3m
. Đồ thị hàm số có
5
điểm cực trị. Nhận.
TH3:
3 6m
. Đồ thị hàm số có
5
điểm cực trị. Nhận.
TH4:
6m&
. Đồ thị hàm số có
3
điểm cực trị. Loại.
Vậy
3 6m$
. Do
*
m
nên
3;4;5m
.
Vậy tổng giá trị tất cả các phần tử của
S
bằng
12
.
Câu 5: (THTT Số 1-484 tháng 10 năm 2017-2018) Tìm tất cả các giá trị thực của tham số
m
để hàm số
3 2
sin 3cos sin 1y x x m x
đồng biến trên đoạn
0; 2
'
!
(
"
.
A.
3m
.B.
0m$
.C.
3m$
.D.
0m
.
Lời giải
Chọn B
Đặt
sin , 0; 0;1
2
x t x t
'
!
(
"
Xét hàm số
3 2
3 4f t t t mt
Ta có
2
3 6f t t t m
Để hàm số
f t
đồng biến trên
0;1
cần:
2 2
0 0;1 3 6 0 0;1 3 6 0;1f t t t t m t t t m t
& # & # &
Xét hàm số
2
3 6g t t t
6 6
0 1
g t t
g t t
#
Bảng biến thiên
x
x
TH1: 0 3m TH2 : 3m
x
x
TH3:3 6m
TH4 : 6m&
Nhìn vào bảng biến thiên ta thấy với
0m$
thì hàm số
f t
đồng biến trên
0;1
, hàm số
f x
đồng biến trên đoạn
0; 2
'
!
(
"
.
Câu 6: (THPT Chuyên Quang Trung-Bình Phước-lần 1-năm 2017-2018) Cho hàm số
3
2
3 4
3
x
y ax ax
. Để hàm số đạt cực trị tại
1
x
,
2
x
thỏa mãn
22
1 2
2 2
2 1
2 9 2
2 9
x ax a a
a x ax a
thì
a
thuộc khoảng nào ?
A.
5
3; 2
a
. B.
7
5; 2
a
. C.
2; 1a
. D.
7; 3
2
a
.
Lời giải
Chọn B
Đạo hàm :
2
2 3y x ax a
,
2
0 2 3 0y x ax a
#
1
Hàm số có hai cực trị
1
x
,
2
x
khi
0y
có hai nghiệm phân biệt
0 3 0a a
# % # )
.
Khi đó
1
x
,
2
x
là nghiệm pt
1
, theo định lý Viet :
1 2
1 2
2
. 3
x x a
x x a
.
Do đó :
2
2 2 2
1 2 1 1 2 2 1 2 1 2
2
2 2 2
2 1 2 1 2 1 1 2 1 2
2 9 3 4 12
2 9 3 4 12
x ax a x x x x x x x x a a
x ax a x x x x x x x x a a
.
Theo đề bài, ta có :
4 12 4 12
2 1 4
4 12
a a a a
a a a
# #
.
Câu 7: (THPT Chuyên Thái Bình-lần 1-năm 2017-2018) Cho hàm số
y f x
có đạo
hàm trên
*
. Đường cong trong hình vẽ bên là đồ thị hàm số
y f x
, (
y f x
liên tục
trên
*
). Xét hàm số
2
2g x f x
. Mệnh đề nào dưới đây sai?
A. Hàm số
g x
nghịch biến trên khoảng
; 2
.
Ox
y
2
2
4
1
1
B. Hàm số
g x
đồng biến trên khoảng
2;
.
C. Hàm số
g x
nghịch biến trên khoảng
1;0
.
D. Hàm số
g x
nghịch biến trên khoảng
0;2
.
Lời giải
Chọn C
Từ đồ thị thấy
1
02
x
f x x
#
và
0 2f x x
#
.
Xét
2
2g x f x
có TXĐ
D*
.
2g x xf t
với
2
2t x
.
2
2
00
0 2 1 1
2
2 2
xx
g x t x x
x
t x
# # +
+
.
Có
2
0 2 2 2 2f t t x x x
# # ,
.
Bảng biến thiên:
Hàm số
g x
đồng biến trên
2;0
.Vậy C sai.
Câu 8: (THPT Lê Hồng Phong-Nam Định-lần 1-năm 2017-2018) Cho hàm số
1
2
x
yx
.
Số các giá trị tham số
m
để đường thẳng
y x m
luôn cắt đồ thị hàm số tại hai điểm phân biệt
A
,
B
sao cho trọng tâm tam giác
OAB
nằm trên đường tròn
2 2
3 4x y y
là
A.
1
. B.
0
.C.
3
.D.
2
.
Lời giải
Chọn D
Phương trình hoành độ giao điểm :
2
13 2 1 0 *
2
xx m x m x m
x
#
Theo yêu cầu bài toán :
*
phải có hai nghiệm phân biệt khác
2
2
02 13 0,
4 3 2 2 1 0 m m m
m m
%
#
Gọi
1 1
;A x y
,
2 2
;B x y
suy ra
G
là trọng tâm của tam giác
OAB
:
1 2 1 2 1 2 1 2
2 3 3 2 3 3
; ; ; ;
3 3 3 3 3 3 3 3
x x y y x x x x m m m m m m
G G G G
Theo yêu cầu bài toán :
2 2
2
3
3 3 3
3 4 2 9 45 0 15
3 3 3 2
m
m m m m m m
# #
.
Câu 9: (THPT Lê Hồng Phong-Nam Định-lần 1-năm 2017-2018) Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
và
BC a
. Cạnh bên
SA
vuông góc với đáy
ABC
. Gọi
có thể bạn quan tâm
Trắc nghiệm có lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng...
6
987
439
Tài liệu, đề thi THPT các trường
6
(New)
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng...
6
983
338
Tài liệu, đề thi THPT các trường
6
(New)
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng...
6
835
333
Tài liệu, đề thi THPT các trường
6
(New)
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng...
39
777
353
Tài liệu, đề thi THPT các trường
39
(New)
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng...
39
997
505
Tài liệu, đề thi THPT các trường
39
(New)
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng...
77
819
556
Tài liệu, đề thi môn Toán
77
(New)
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng...
28
930
267
Tài liệu, đề thi môn Toán
28
(New)
Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng...
6
759
333
Tài liệu, đề thi THPT các trường
6
(New)
thông tin tài liệu
Tổng hợp các dạng bài tập Trắc nghiệm và lời giải toán 12 chương 1 Khảo sát hàm số: Chương 1 Ứng dụng đạo hàm - Mức độ 4 phần 1
Mở rộng để xem thêm
tài liệu mới trong mục này
Giải bài tập trang 144 SGK Hóa lớp 9: Mối liên hệ giữa etilen, rượu etylic và axit axetic
Giải bài tập Hóa lớp 9: Rượu etylic
Giải bài tập Hóa lớp 9: Khái niệm về hợp chất hữu cơ và hoá học hữu cơ
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm giá trị phần trăm một số
Tóm tắt lý thuyết Toán lớp 5: Giải toán về tỉ số phần trăm. Tìm tỉ số phần trăm của hai số
tài liệu hot trong mục này
Ôn tập kiến thức môn Toán lớp 2 chuyên đề: Phép cộng có nhớ
Bộ đề thi giữa học kì 1 môn Toán lớp 2 theo Thông tư 22
Một số dạng bài tập về Phép cộng, trừ các số nguyên trong chương trình Toán lớp 6
Bài tập ôn tập cuối tuần lớp 2: Tuần 21
Lý thuyết và một số dạng bài tập về Lũy thừa với số mũ tự nhiên và các phép toán (Toán lớp 6)
tài liệu giúp tôi
Nếu bạn không tìm thấy tài liệu mình cần có thể gửi yêu cầu ở đây để chúng tôi tìm giúp bạn!
xem nhiều trong tuần
Giáo trình Quản trị học của Đại học kinh tế quốc dân
4 đề thi học sinh giỏi Toán lớp 2, có đáp án kèm theo
MẪU GIỚI THIỆU CHUYỂN SINH HOẠT HỘI
PHÂN TÍCH CHUỖI CUNG ỨNG CỦA COCA COLA VIỆT NAM
Địa lý 12 Phát triển cây công nghiệp lâu năm Tây Nguyên
IOE tiếng Anh lớp 10 lần 21 niên khóa 2016
yêu cầu tài liệu
Giúp bạn tìm tài liệu chưa có
×
